[tds-section background="#000000" textcolor="#FFFFFF" opacity="80"]

Cet article fait partie de nos archives. Vous cherchez des solutions à vos problèmes ou des infos sur une version plus récente?
Parcourez SUR CETTE PAGE l'ensemble des articles de nos experts à propos d’INVENTOR (dernières et anciennes versions)!

[/tds-section]
[tds-divider invisible thickness=40]

Tutorial Inventor Simulation (RDM) : flexion poutre

Poutre reposant sur deux appuis avec charge concentrée au milieu

Cas simple de détermination de l'équation de la déformée d'une poutre en flexion plane.
Hypothèses :
- les appuis sont sans adhérence.
- les charges sont perpendiculaires à la ligne moyenne.

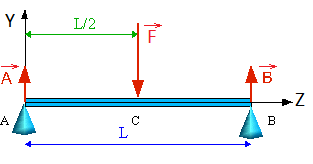 Les efforts sont tels que: A = B = F/2

Avec :

y= flèche en mm
F = charge en N
L = longueur entre les appuis en mm
E = module d'Young en N/mm²
I = moment d'inertie de la section de la poutre en mm⁴

Prenons l'exemple d'un profilé (HEA de 120) depuis le Centre de Contenu NF A 45-201 - HE 120 A de longueur L= 5000 mm

Avec F=8000 N,  E=210000n/mm²,  I=Ix=6061516  mm⁴

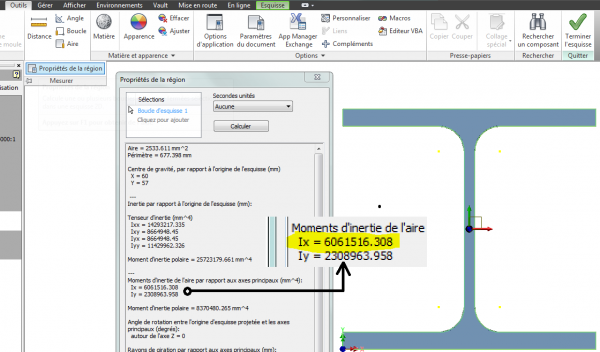
ƒ= - ( 8000 x ( 5000 )³ ) / ( 48 x 210000 x 6061516 ) = 16 mm

Vérifions à l'aide du calcul par éléments finis
(donc sans utiliser le calcul sur ossature inclus lui aussi dans Inventor Professional 2013)

Plaçons la Force F = 8000 N sur la face supérieure du profilé, puis bloquons les 2 arêtes inférieures des 2 extrémités du profilé.

Nous obtenons une flèche (déplacement sur l'Axe Y) de 9.66 mm qui est bien différente de celle obtenue par le calcul théorique.

ƒ= - ( 8000 x ( 5000 )³ ) / ( 48 x 210000 x 6061516 ) = - 16 mm

Pourquoi une telle différence ?

Voici les pièges d'applications des contraintes et des appuis dans cet exemple simple.

La charge F a été appliquée sur toute la face (et non pas au centre de celle-ci) ce qui est l'équivalent à une charge de 8000 N uniformément répartie sur toute la longueur L.

soit un calcul de type ƒ=5qL⁴ / 384 EI avec q = 8000 N / 5000 mm  soit 1.6 N / mm.

soit  ƒ= - 5 ( 1.6x ( 5000 )⁴ ) / ( 384 x 210000 x 6061516 ) = - 10 mm

Il faut aussi libérer le déplacement en Z sur l'un des support fixes (sur B)

Il faut scinder la face à l'aide d'une esquisse circulaire afin d'appliquer la charge P sur la centre de la poutre.

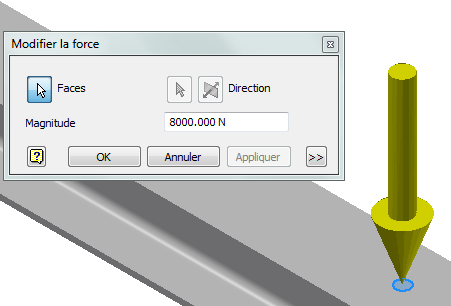
Après les 2 modifications (Charge appliquée sur la petite face obtenue par la scission et appui sur la point B avec déplacement sur Z possible)

Nous obtenons maintenant un résultat de 16.36 mm qui est très proche du calcul théorique de 16 mm.